Disclaimer
Redistribution and use of this article, any part of it or any images or files referenced in it, in source and binary forms, with or without modification, are permitted provided that the following conditions are met:
- Redistributions of article must retain the above copyright notice, this list of conditions, link to this page (https://xdevs.com/article/rnet_ratio/) and the following disclaimer.
- Redistributions of files in binary form must reproduce the above copyright notice, this list of conditions, link to this page (https://xdevs.com/article/rnet_ratio/), and the following disclaimer in the documentation and/or other materials provided with the distribution, for example Readme file.
All information posted here is hosted just for education purposes and provided AS IS. In no event shall the author, xDevs.com site, or any other 3rd party be liable for any special, direct, indirect, or consequential damages or any damages whatsoever resulting from loss of use, data or profits, whether in an action of contract, negligence or other tortuous action, arising out of or in connection with the use or performance of information published here.
If you willing to contribute or add your experience regarding instrument repairs or provide extra information, you can do so following these simple instructions.
Motivation for this work
Resistor network series such as Linear LT5400, TDP1603, NOMCA1603, TOMC1603, ORN and many more are known to have good temperature coefficient tracking and some of them also have quite low 1/f noise [1], [2].
On the other hand dividers are needed when it comes to voltage reference circuits around famous Linear LTZ1000 SuperZener for either setting the operating temperature of the internal oven or scaling of the output voltage. In [3] a ratio of 13:1 is shown to set the oven temperature to +60 °C. Although the divider is given with exact numbers for the resistors actually only the ratio is most important and fractions or multiple of that resistors forming the same ratio would lead to the same results.
By now most of the circuits presented used either various precision wirewound resistors or fixed ratio dividers such as metal foil VHD200 from VPG in hermetically sealed package, with ratios such as 13:1 or similar. These dividers with no doubt are superior in either temperature coefficient tracking and noise, but very expensive ($30 and more USD per unit) and the lead-time of 6+ months is quite long for experimental circuits. On positive note, any custom ratio is possible to order. Nevertheless, getting a complete and trimmed 10V DC voltage reference based on such custom parts up and running can take almost forever and is thus not practical for many applications.
The aforementioned networks are cheap and easy to score from several distributors. Though, only a few engineers are aware of what is possible with only N nominally equal valued resistors.
In reference [4] an equivalent resistance made by N equal resistors is discussed. Based on the results presented it can be concluded that resistive dividers can be made out of combinations of serial, parallel, bridge and cascade connections of N equal resistors, too. Since such combinations also allow for different taps within the same resistor arrangement even and odd divider ratios can be created to whatever is needed.
The most common approach is to arrange the resistors in a fashion, that the resulting network matches the absolute values as given e.g. per datasheet of the LTZ reference circuit. As already discussed this is not needed, as mostly the ratio is important.
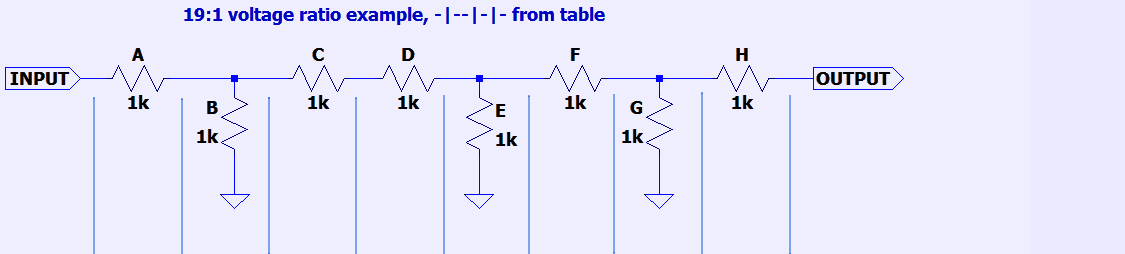
The encoding example is shown in Table 1. Symbols are used to show if resistor connected in series with signal path or connected to reference (ground symbol in schematics representation). Signal path is always from left Input (resistor A) to right Output (resistor H).
- — mean resistor is in series connection
- | mean resistor is referenced to ground (reference)
- = mean 2 resistors in parallel (used in non-integer ratios)
Table 2 highlights some of the possible ratios already found with up to 8 equal resistors. The results found use cascades as well as serial and parallel connections in a limited extend only. Thus, the table is far away from being complete and having an algorithm available to find all possible combinations is one of the current tasks.
| Resistor A | Resistor B | Resistor C | Resistor D | Resistor E | Resistor F | Resistor G | Resistor H | Voltage ratio | Resistance ratio |
|---|---|---|---|---|---|---|---|---|---|
| — | | | — | — | | | — | | | — | 19:1 | 18:1 |
Table 1: Example encoding of ratio network for 19:1 voltage output
Other integer ratios shown in table below.
| Resistor A | Resistor B | Resistor C | Resistor D | Resistor E | Resistor F | Resistor G | Resistor H | Voltage ratio | Resistance ratio |
|---|---|---|---|---|---|---|---|---|---|
| — | — | — | — | — | — | — | — | 1:1 | |
| — | — | — | — | — | — | — | | | 8:1 | 7:1 |
| — | — | — | — | — | — | | | — | 7:1 | 6:1 |
| — | — | — | — | — | — | | | | | 13:1 | 12:1 |
| — | — | — | — | — | | | — | — | 6:1 | 5:1 |
| — | — | — | — | — | | | — | | | 17:1 | 16:1 |
| — | — | — | — | — | | | | | — | 11:1 | 10:1 |
| — | — | — | — | — | | | | | | | 16:1 | 15:1 |
| — | — | — | — | | | — | — | — | 5:1 | 4:1 |
| — | — | — | — | | | — | — | | | 19:1 | 18:1 |
| — | — | — | — | | | — | | | — | 14:1 | 13:1 |
| — | — | — | — | | | — | | | | | 23:1 | 22:1 |
| — | — | — | — | | | | | — | — | 9:1 | 8:1 |
| — | — | — | — | | | | | — | | | 22:1 | 21:1 |
| — | — | — | — | | | | | | | — | 13:1 | 12:1 |
| — | — | — | — | | | | | | | | | 17:1 | 16:1 |
| — | — | — | | | — | — | — | — | 4:1 | 3:1 |
| — | — | — | | | — | — | — | | | 19:1 | 18:1 |
| — | — | — | | | — | — | | | — | 15:1 | 14:1 |
| — | — | — | | | — | — | | | | | 26:1 | 25:1 |
| — | — | — | | | — | | | — | — | 11:1 | 10:1 |
| — | — | — | | | — | | | — | | | 29:1 | 28:1 |
| — | — | — | | | — | | | | | — | 18:1 | 17:1 |
| — | — | — | | | — | | | | | | | 25:1 | 24:1 |
| — | — | — | | | | | — | — | — | 7:1 | 6:1 |
| — | — | — | | | | | — | — | | | 24:1 | 23:1 |
| — | — | — | | | | | — | | | — | 17:1 | 16:1 |
| — | — | — | | | | | — | | | | | 27:1 | 26:1 |
| — | — | — | | | | | | | — | — | 10:1 | 9:1 |
| — | — | — | | | | | | | — | | | 23:1 | 22:1 |
| — | — | — | | | | | | | | | — | 13:1 | 12:1 |
| — | — | — | | | | | | | | | | | 16:1 | 15:1 |
| — | — | | | — | — | — | — | — | 3:1 | 2:1 |
| — | — | | | — | — | — | — | | | 17:1 | 16:1 |
| — | — | | | — | — | — | | | — | 14:1 | 13:1 |
| — | — | | | — | — | — | | | | | 25:1 | 24:1 |
| — | — | | | — | — | | | — | — | 11:1 | 10:1 |
| — | — | | | — | — | | | — | | | 30:1 | 29:1 |
| — | — | | | — | — | | | | | — | 19:1 | 18:1 |
| — | — | | | — | — | | | | | | | 27:1 | 26:1 |
| — | — | | | — | | | — | — | — | 8:1 | 7:1 |
| — | — | | | — | | | — | — | | | 29:1 | 28:1 |
| — | — | | | — | | | — | | | — | 21:1 | 20:1 |
| — | — | | | — | | | — | | | | | 34:1 | 33:1 |
| — | — | | | — | | | | | — | — | 13:1 | 12:1 |
| — | — | | | — | | | | | — | | | 31:1 | 30:1 |
| — | — | | | — | | | | | | | — | 18:1 | 17:1 |
| — | — | | | — | | | | | | | | | 23:1 | 22:1 |
| — | — | | | | | — | — | — | — | 5:1 | 4:1 |
| — | — | | | | | — | — | — | | | 22:1 | 21:1 |
| — | — | | | | | — | — | | | — | 17:1 | 16:1 |
| — | — | | | | | — | — | | | | | 29:1 | 28:1 |
| — | — | | | | | — | | | — | — | 12:1 | 11:1 |
| — | — | | | | | — | | | — | | | 31:1 | 30:1 |
| — | — | | | | | — | | | | | — | 19:1 | 18:1 |
| — | — | | | | | — | | | | | | | 26:1 | 25:1 |
| — | — | | | | | | | — | — | — | 7:1 | 6:1 |
| — | — | | | | | | | — | — | | | 23:1 | 22:1 |
| — | — | | | | | | | — | | | — | 16:1 | 15:1 |
| — | — | | | | | | | — | | | | | 25:1 | 24:1 |
| — | — | | | | | | | | | — | — | 9:1 | 8:1 |
| — | — | | | | | | | | | — | | | 20:1 | 19:1 |
| — | — | | | | | | | | | | | — | 11:1 | 10:1 |
| — | — | | | | | | | | | | | | | 13:1 | 12:1 |
| — | | | — | — | — | — | — | — | 2:1 | 1:1 |
| — | | | — | — | — | — | — | | | 13:1 | 12:1 |
| — | | | — | — | — | — | | | — | 11:1 | 10:1 |
| — | | | — | — | — | — | | | | | 20:1 | 19:1 |
| — | | | — | — | — | | | — | — | 9:1 | 8:1 |
| — | | | — | — | — | | | — | | | 25:1 | 24:1 |
| — | | | — | — | — | | | | | — | 16:1 | 15:1 |
| — | | | — | — | — | | | | | | | 23:1 | 22:2 |
| — | | | — | — | | | — | — | — | 7:1 | 6:1 |
| — | | | — | — | | | — | — | | | 26:1 | 25:1 |
| — | | | — | — | | | — | | | — | 19:1 | 18:1 |
| — | | | — | — | | | — | | | | | 31:1 | 30:1 |
| — | | | — | — | | | | | — | — | 12:1 | 11:1 |
| — | | | — | — | | | | | — | | | 29:1 | 28:1 |
| — | | | — | — | | | | | | | — | 17:1 | 16:1 |
| — | | | — | — | | | | | | | | | 22:1 | 21:1 |
| — | | | — | | | — | — | — | — | 5:1 | 4:1 |
| — | | | — | | | — | — | — | | | 23:1 | 22:1 |
| — | | | — | | | — | — | | | — | 18:1 | 18:1 |
| — | | | — | | | — | — | | | | | 31:1 | 30:1 |
| — | | | — | | | — | | | — | — | 13:1 | 12:1 |
| — | | | — | | | — | | | — | | | 34:1 | 33:1 |
| — | | | — | | | — | | | | | — | 21:1 | 20:1 |
| — | | | — | | | — | | | | | | | 29:1 | 28:1 |
| — | | | — | | | | | — | — | — | 8:1 | 7:1 |
| — | | | — | | | | | — | — | | | 27:1 | 26:1 |
| — | | | — | | | | | — | | | — | 19:1 | 18:1 |
| — | | | — | | | | | — | | | | | 30:1 | 29:1 |
| — | | | — | | | | | | | — | — | 11:1 | 10:1 |
| — | | | — | | | | | | | — | | | 25:1 | 24:1 |
| — | | | — | | | | | | | | | — | 14:1 | 13:1 |
| — | | | — | | | | | | | | | | | 17:1 | 16:1 |
| — | | | | | — | — | — | — | — | 3:1 | 2:1 |
| — | | | | | — | — | — | — | | | 16:1 | 15:1 |
| — | | | | | — | — | — | | | — | 13:1 | 12:1 |
| — | | | | | — | — | — | | | | | 23:1 | 22:1 |
| — | | | | | — | — | | | — | — | 10:1 | 9:1 |
| — | | | | | — | — | | | — | | | 27:1 | 26:1 |
| — | | | | | — | — | | | | | — | 17:1 | 16:1 |
| — | | | | | — | — | | | | | | | 24:1 | 23:1 |
| — | | | | | — | | | — | — | — | 7:1 | 6:1 |
| — | | | | | — | | | — | — | | | 25:1 | 24:1 |
| — | | | | | — | | | — | | | — | 18:1 | 17:1 |
| — | | | | | — | | | — | | | | | 29:1 | 28:1 |
| — | | | | | — | | | | | — | — | 11:1 | 10:1 |
| — | | | | | — | | | | | — | | | 26:1 | 25:1 |
| — | | | | | — | | | | | | | — | 15:1 | 14:1 |
| — | | | | | — | | | | | | | | | 19:1 | 18:1 |
| — | | | | | | | — | — | — | — | 4:1 | 3:1 |
| — | | | | | | | — | — | — | | | 17:1 | 16:1 |
| — | | | | | | | — | — | | | — | 13:1 | 12:1 |
| — | | | | | | | — | — | | | | | 22:1 | 21:1 |
| — | | | | | | | — | | | — | — | 9:1 | 8:1 |
| — | | | | | | | — | | | — | | | 23:1 | 22:1 |
| — | | | | | | | — | | | | | — | 14:1 | 13:1 |
| — | | | | | | | — | | | | | | | 19:1 | 18:1 |
| — | | | | | | | | | — | — | — | 5:1 | 4:1 |
| — | | | | | | | | | — | — | | | 16:1 | 15:1 |
| — | | | | | | | | | — | | | — | 11:1 | 10:1 |
| — | | | | | | | | | — | | | | | 17:1 | 16:1 |
| — | | | | | | | | | | | — | — | 6:1 | 5:1 |
| — | | | | | | | | | | | — | | | 13:1 | 12:1 |
| — | | | | | | | | | | | | | — | 7:1 | 6:1 |
| — | | | | | | | | | | | | | | | 8:1 | 7:1 |
| | | — | — | — | — | — | — | — | 1:1 | |
| | | — | — | — | — | — | — | | | 7:1 | 6:1 |
| | | — | — | — | — | — | | | — | 6:1 | 5:1 |
| | | — | — | — | — | — | | | | | 11:1 | 10:1 |
| | | — | — | — | — | | | — | — | 5:1 | 4:1 |
| | | — | — | — | — | | | — | | | 14:1 | 13:1 |
| | | — | — | — | — | | | | | — | 9:1 | 8:1 |
| | | — | — | — | — | | | | | | | 13:1 | 12:1 |
| | | — | — | — | | | — | — | — | 4:1 | 3:1 |
| | | — | — | — | | | — | — | | | 15:1 | 14:1 |
| | | — | — | — | | | — | | | — | 11:1 | 10:1 |
| | | — | — | — | | | — | | | | | 18:1 | 17:1 |
| | | — | — | — | | | | | — | — | 7:1 | 6:1 |
| | | — | — | — | | | | | — | | | 17:1 | 16:1 |
| | | — | — | — | | | | | | | — | 10:1 | 9:1 |
| | | — | — | — | | | | | | | | | 13:1 | 12:1 |
| | | — | — | | | — | — | — | — | 3:1 | 2:1 |
| | | — | — | | | — | — | — | | | 14:1 | 13:1 |
| | | — | — | | | — | — | | | — | 11:1 | 10:1 |
| | | — | — | | | — | — | | | | | 19:1 | 18:1 |
| | | — | — | | | — | | | — | — | 8:1 | 7:1 |
| | | — | — | | | — | | | — | | | 21:1 | 20:1 |
| | | — | — | | | — | | | | | — | 13:1 | 12:1 |
| | | — | — | | | — | | | | | | | 18:1 | 17:1 |
| | | — | — | | | | | — | — | — | 5:1 | 4:1 |
| | | — | — | | | | | — | — | | | 17:1 | 16:1 |
| | | — | — | | | | | — | | | — | 12:1 | 11:1 |
| | | — | — | | | | | — | | | | | 19:1 | 18:1 |
| | | — | — | | | | | | | — | — | 7:1 | 6:1 |
| | | — | — | | | | | | | — | | | 16:1 | 15:1 |
| | | — | — | | | | | | | | | — | 9:1 | 8:1 |
| | | — | — | | | | | | | | | | | 11:1 | 10:1 |
| | | — | | | — | — | — | — | — | 2:1 | 1:1 |
| | | — | | | — | — | — | — | | | 11:1 | 10:1 |
| | | — | | | — | — | — | | | — | 9:1 | 8:1 |
| | | — | | | — | — | — | | | | | 16:1 | 15:1 |
| | | — | | | — | — | | | — | — | 7:1 | 6:1 |
| | | — | | | — | — | | | — | | | 19:1 | 18:1 |
| | | — | | | — | — | | | | | — | 12:1 | 11:1 |
| | | — | | | — | — | | | | | | | 17:1 | 16:1 |
| | | — | | | — | | | — | — | — | 5:1 | 4:1 |
| | | — | | | — | | | — | — | | | 18:1 | 17:1 |
| | | — | | | — | | | — | | | — | 13:1 | 12:1 |
| | | — | | | — | | | — | | | | | 21:1 | 20:1 |
| | | — | | | — | | | | | — | — | 8:1 | 7:1 |
| | | — | | | — | | | | | — | | | 19:1 | 18:1 |
| | | — | | | — | | | | | | | — | 11:1 | 10:1 |
| | | — | | | — | | | | | | | | | 14:1 | 13:1 |
| | | — | | | | | — | — | — | — | 3:1 | 2:1 |
| | | — | | | | | — | — | — | | | 13:1 | 12:1 |
| | | — | | | | | — | — | | | — | 10:1 | 9:1 |
| | | — | | | | | — | — | | | | | 17:1 | 16:1 |
| | | — | | | | | — | | | — | — | 7:1 | 6:1 |
| | | — | | | | | — | | | — | | | 18:1 | 17:1 |
| | | — | | | | | — | | | | | — | 11:1 | 10:1 |
| | | — | | | | | — | | | | | | | 15:1 | 14:1 |
| | | — | | | | | | | — | — | — | 4:1 | 3:1 |
| | | — | | | | | | | — | — | | | 13:1 | 12:1 |
| | | — | | | | | | | — | | | — | 9:1 | 8:1 |
| | | — | | | | | | | — | | | | | 14:1 | 13:1 |
| | | — | | | | | | | | | — | — | 5:1 | 4:1 |
| | | — | | | | | | | | | — | | | 11:1 | 10:1 |
| | | — | | | | | | | | | | | — | 6:1 | 5:1 |
| | | — | | | | | | | | | | | | | 7:1 | 6:1 |
| | | | | — | — | — | — | — | — | 1:1 | |
| | | | | — | — | — | — | — | | | 6:1 | 5:1 |
| | | | | — | — | — | — | | | — | 5:1 | 4:1 |
| | | | | — | — | — | — | | | | | 9:1 | 8:1 |
| | | | | — | — | — | | | — | — | 4:1 | 3:1 |
| | | | | — | — | — | | | — | | | 11:1 | 10:1 |
| | | | | — | — | — | | | | | — | 7:1 | 6:1 |
| | | | | — | — | — | | | | | | | 10:1 | 9:1 |
| | | | | — | — | | | — | — | — | 3:1 | 2:1 |
| | | | | — | — | | | — | — | | | 11:1 | 10:1 |
| | | | | — | — | | | — | | | — | 8:1 | 7:1 |
| | | | | — | — | | | — | | | | | 13:1 | 12:1 |
| | | | | — | — | | | | | — | — | 5:1 | 4:1 |
| | | | | — | — | | | | | — | | | 12:1 | 11:1 |
| | | | | — | — | | | | | | | — | 7:1 | 6:1 |
| | | | | — | — | | | | | | | | | 9:1 | 8:1 |
| | | | | — | | | — | — | — | — | 2:1 | 1:1 |
| | | | | — | | | — | — | — | | | 9:1 | 8:1 |
| | | | | — | | | — | — | | | — | 7:1 | 7:1 |
| | | | | — | | | — | — | | | | | 12:1 | 11:1 |
| | | | | — | | | — | | | — | — | 5:1 | 4:1 |
| | | | | — | | | — | | | — | | | 13:1 | 12:1 |
| | | | | — | | | — | | | | | — | 8:1 | 7:1 |
| | | | | — | | | — | | | | | | | 11:1 | 10:1 |
| | | | | — | | | | | — | — | — | 3:1 | 2:1 |
| | | | | — | | | | | — | — | | | 10:1 | 9:1 |
| | | | | — | | | | | — | | | — | 7:1 | 6:1 |
| | | | | — | | | | | — | | | | | 11:1 | 10:1 |
| | | | | — | | | | | | | — | — | 4:1 | 3:1 |
| | | | | — | | | | | | | — | | | 9:1 | 8:1 |
| | | | | — | | | | | | | | | — | 5:1 | 4:1 |
| | | | | — | | | | | | | | | | | 6:1 | 5:1 |
| | | | | | | — | — | — | — | — | 1:1 | |
| | | | | | | — | — | — | — | | | 5:1 | 4:1 |
| | | | | | | — | — | — | | | — | 4:1 | 3:1 |
| | | | | | | — | — | — | | | | | 7:1 | 6:1 |
| | | | | | | — | — | | | — | — | 3:1 | 2:1 |
| | | | | | | — | — | | | — | | | 8:1 | 7:1 |
| | | | | | | — | — | | | | | — | 5:1 | 4:1 |
| | | | | | | — | — | | | | | | | 7:1 | 6:1 |
| | | | | | | — | | | — | — | — | 2:1 | 1:1 |
| | | | | | | — | | | — | — | | | 7:1 | 6:1 |
| | | | | | | — | | | — | | | — | 5:1 | 4:1 |
| | | | | | | — | | | — | | | | | 8:1 | 7:1 |
| | | | | | | — | | | | | — | — | 3:1 | 2:1 |
| | | | | | | — | | | | | — | | | 7:1 | 6:1 |
| | | | | | | — | | | | | | | — | 4:1 | 3:1 |
| | | | | | | — | | | | | | | | | 5:1 | 4:1 |
| | | | | | | | | — | — | — | — | 1:1 | |
| | | | | | | | | — | — | — | | | 4:1 | 3:1 |
| | | | | | | | | — | — | | | — | 3:1 | 2:1 |
| | | | | | | | | — | — | | | | | 5:1 | 4:1 |
| | | | | | | | | — | | | — | — | 2:1 | 1:1 |
| | | | | | | | | — | | | — | | | 5:1 | 4:1 |
| | | | | | | | | — | | | | | — | 3:1 | 2:1 |
| | | | | | | | | — | | | | | | | 4:1 | 3:1 |
| | | | | | | | | | | — | — | — | 1:1 | |
| | | | | | | | | | | — | — | | | 3:1 | 2:1 |
| | | | | | | | | | | — | | | — | 2:1 | 1:1 |
| | | | | | | | | | | — | | | | | 3:1 | 2:1 |
| | | | | | | | | | | | | — | — | 1:1 | |
| | | | | | | | | | | | | — | | | 2:1 | 1:1 |
| | | | | | | | | | | | | | | — | 1:1 | |
| | | | | | | | | | | | | | | | | 1:1 |
Table 2: Various configurations for integer ratios
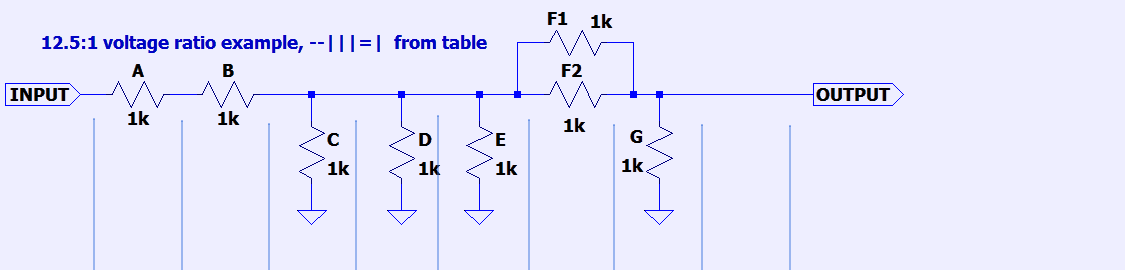
Making ratios with non-integer values require connecting some resistor elements in parallel. This is bit harder to calculate in 8-resistor networks, so some examples common for LTZ1000 reference circuits presented in Table 3 as starting example.
Just like previous table for integer ratios signal path here always from left Input (resistor A) to right Output (resistor G, as H is no more available).
- — mean resistor is in series connection
- | mean resistor is referenced to ground (reference)
- = mean 2 resistors in parallel (used in non-integer ratios)
| Resistor A | Resistor B | Resistor C | Resistor D | Resistor E | Resistor F | Resistor G | Resistor H | Voltage ratio | Resistance ratio |
|---|---|---|---|---|---|---|---|---|---|
| = | — | | | — | | | | | — | 10.5:1 | 9.5:1 | |
| — | = | | | — | | | | | — | 10.5:1 | 9.5:1 | |
| = | — | — | — | | | | | | | 11.5:1 | 10.5:1 | |
| — | = | — | — | | | | | | | 11.5:1 | 10.5:1 | |
| — | — | = | — | | | | | | | 11.5:1 | 10.5:1 | |
| — | — | — | = | | | | | | | 11.5:1 | 10.5:1 | |
| — | — | — | — | | | = | | | 11.5:1 | 10.5:1 | |
| = | — | — | — | | | — | | | 12.5:1 | 11.5:1 | |
| — | = | — | — | | | — | | | 12.5:1 | 11.5:1 | |
| — | — | = | — | | | — | | | 12.5:1 | 11.5:1 | |
| — | — | — | = | | | — | | | 12.5:1 | 11.5:1 | |
| = | — | | | | | | | — | | | 12.5:1 | 11.5:1 | |
| — | = | | | | | | | — | | | 12.5:1 | 11.5:1 | |
| — | — | | | | | | | = | | | 12.5:1 | 11.5:1 | |
| = | — | — | | | — | — | | | 13:1 | 12:1 | |
| — | = | — | | | — | — | | | 13:1 | 12:1 | |
| — | — | = | | | — | — | | | 13:1 | 12:1 | |
| — | — | — | | | = | — | | | 13:1 | 12:1 | |
| — | — | — | | | — | = | | | 13:1 | 12:1 | |
| — | — | | | = | | | | | | | 13.5:1 | 12.5:1 | |
| — | — | — | | | | | = | | | 13.5:1 | 12.5:1 | |
| — | — | | | | | = | | | | | 14:1 | 13:1 | |
| — | — | — | | | = | | | | | 14:1 | 13:1 | |
| = | — | — | | | | | — | | | 14.5:1 | 13.5:1 | |
| — | = | — | | | | | — | | | 14.5:1 | 13.5:1 | |
| — | — | = | | | | | — | | | 14.5:1 | 13.5:1 | |
| = | — | — | | | — | | | | | 15.5:1 | 14.5:1 | |
| — | = | — | | | — | | | | | 15.5:1 | 14.5:1 | |
| — | — | = | | | — | | | | | 15.5:1 | 14.5:1 |
Table 3: Some of the non-integer ratios with paralleled resistors
This article is also available in PDF-format
Discussion is very welcome thru comment section or at our own IRC chat server: irc.xdevs.com (standard port 6667, channel: #xDevs.com). Web-interface for access mirrored on this page.
Modified: Feb. 19, 2022, 4:06 p.m.
